Click to view our Accessibility Statement or contact us with accessibility-related questions













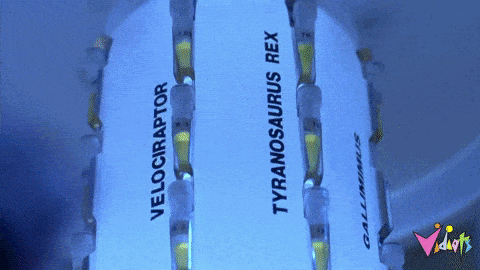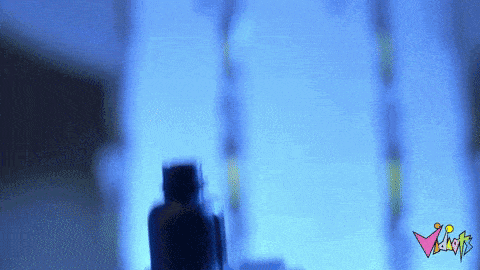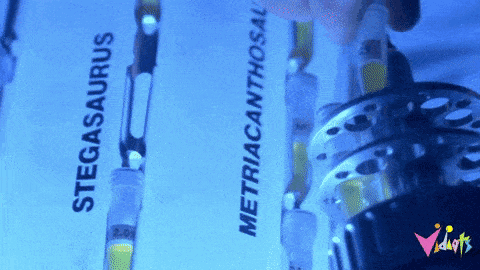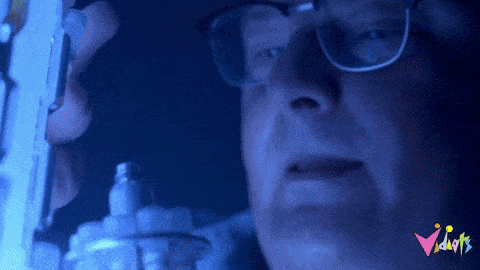
mStone Custom Gold-Plated Mechanical Switch Springs
mStone Custom Gold-Plated Mechanical Switch Springs
bookmark_border
Where's the price?
To negotiate the best possible price for our customers, we agree to hide prices prior to logging in.
119 requests
·
105 Sold
Product Description
Out of every switch component, the spring is perhaps the most instrumental in creating a switch’s individual feel. No matter what your preference is, mStone’s custom gold-plated switch spring line has the fine-tuned, high-performing feel you’re after Read More

search
close
Sort by: Newest
keyboard_arrow_down
LifelongCaboose
601
Oct 18, 2021
I don't know why I was expecting the jars to be small, I know the size of springs. But there are some pretty large plastic jars. 3 1/2" by 2". Sadly the metal lids on mine were pretty scratched up, they also have huge barcode stickers on the top that once removed leave a lot of glue. It kind of defeats the purpose of having nice packaging.
The spring length and weight are listed on the bottom where the barcode should be. They all also have a safety seal which I thought was funny, since it wasn't even sealed on and their springs. Once Removed from the nice roll of plastic you won't be able to store them back inside so it's just a big waste of plastic. I like the jar as you can reuse that. But the plastic that holds the springs feels very wasteful.
As for the actual product, I have not put them in a full set of switches yet, but using them in a few there are pretty good springs. I would like to buy them again for the quality of the spring and amount of options available. But the packaging is very much a gimmick and is wasteful at the end of the day and only takes up more room on my keyboard parts shelf.
I'd love to see them shipped in smaller jars with no plastic roll.

nataku411
115
Jul 12, 2021
Ok, so for people who don't know how to begin differentiating these lengths apart,
Most LONG springs are around 23mm. Most NORMAL springs are 13-15mm.
Longer springs give switches a more flat rate of weight increase towards the bottom out.(better for tactiles or if you want a similar weight going down for linears)
Shorter springs have a lighter weight that increases as you bottom out.
ALL springs are sold by BOTTOM OUT weight.
If you are considering any of these, I would recommend getting the 23mm springs, since longer springs are becoming heavily favored for how they add a snappier action to tactiles and a more-consistent stroke to linears. Don't worry about how many 'stages' or 'coiled parts' there are. Just focus on what bottom-out weight you think you'd like.
Do remember that the heavier the spring weight, the less tactility you will feel. So if your favorite tactile switch has a 55g NORMAL spring, you don't want to get a heavier LONG spring than that and may want to consider going a tad bit lighter.
(Edited)

nataku411
115
Jul 12, 2021
> I'm assuming that the longer springs have a lower force ramp rate (preload vs. bottom out force is closer together) vs. the shorter ones and therefore are more "linear" in feel
That is correct.
As for the Trues, you would think that a 100g bottom out is tiring but during normal typing you're only using enough force to actuate the switch, but your finger is rebounded by the tremendously heavy spring immediately. Once you start typing you basically tend to not bottom at all.
I would definitely check out my comment to Mito below for more info.
MTBoniface
7
Jul 17, 2021
nataku411That depends. I put 100g springs in Box Navy switches because I was bottoming out with every keystroke.

Shibanuggets
16
Jul 12, 2021
So for any future potential buyers, what is the simple answer? - What difference does Spring Length make?
What would the difference feel like in a 75g 15mm vs 23mm spring?
Duckferd
15
Jul 12, 2021
ShibanuggetsLonger springs typically give a gentler force ramp rate and more linear feel between actuation and bottom out; shorter springs give a sharper force ramp rate and feel more progressive.
An example of a short spring effect is given by another member in the Halo True. This has a 60g spring force around actuation point, but bottom out is 100g. The short spring length means that this allows you to press to actuation point relatively easily, but spring rate quickly increases afterwards (discouraging bottom out). If this were a longer length spring, presumably the actuation and bottom out forces would not be so far apart (60 vs 100), meaning for the same amount of keystroke travel you would get less of a force ramp up rate.

Wolframme
27
Jul 12, 2021
Been waiting patiently for long 20mm+ springs at heavier weights, looks like this is it.

static.overdub
571
Jul 12, 2021
It's great that these are individually packaged. I sell single bespoke and made-to-order springs at my store Spring-a-ding-ding and these will be going in the front display.
ZaghamKarim
1
Aug 21, 2021
static.overdubDo you have a link to the store, couldn't find it online. Would love to see the selection available!

MiTo
13959
MiTo
Jul 11, 2021
Upon reflecting on what I asked myself, I think physically speaking we have to go a bit deeper than what basic observation of Hooke's Law suggests so let's look at the formula:
F = k . x
Whereas:
The more coils we have, lower is the required strength to fully compress the spring. What I am struggling to understand is that Sprit apparently has a bunch of options but in the end many of them are (someone correct me if I am wrong) the same. A 67 g spring requires 67 cN (if I'm not mistaken) of force to gets fully compressed regardless if it is 10 mm or 30 mm long, because Sprit is varying the number of coils in the respective springs. What is the difference between a 67 g 23 mm long spring and a 67 g 15 mm long if not the number of coils used to achieve the same weight? I am very interested in all of these springs and looking to experiment how they feel because there must be something to it, but I am not understanding the logic so if someone could explain I'd appreciate. There is supposedly a graph on Sprit's website: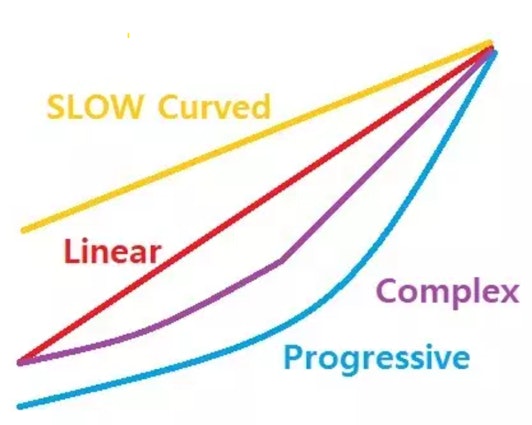
- F = force expressed in Newtons
- k = a constant value
- x = observed length of deformation
- k = constant, the value we want to find
- G = modulus of rigidity of spring material, each material has its own
- d = wire diameter
- n = number of coils
- D = coil diameter
- G, the modulus of rigidity does not change because the entire spring is composed of the same material
- d, you can ignore small variations of wire diameter because in this case they are negligible
- D, coil diameter variations are also negligible since the springs are apparently well constructed
- G.d^4 = A
- 8.n.D^3 = n.8.D^3 = n.B
- A/B = C (save this for later)
The more coils we have, lower is the required strength to fully compress the spring. What I am struggling to understand is that Sprit apparently has a bunch of options but in the end many of them are (someone correct me if I am wrong) the same. A 67 g spring requires 67 cN (if I'm not mistaken) of force to gets fully compressed regardless if it is 10 mm or 30 mm long, because Sprit is varying the number of coils in the respective springs. What is the difference between a 67 g 23 mm long spring and a 67 g 15 mm long if not the number of coils used to achieve the same weight? I am very interested in all of these springs and looking to experiment how they feel because there must be something to it, but I am not understanding the logic so if someone could explain I'd appreciate. There is supposedly a graph on Sprit's website:


nataku411
115
Jul 12, 2021
MiToI've tried and tested every single type of Sprit's springs as well as many long springs from others, and my only true conclusion is that Sprit's ridiculous assortment tries to put names to conventions but only ends up confusing the customer. I was even going to go as far as to rent out a texture/weight graphing machine to graph out force curves, but in the end I quickly discovered that there are only two variables in how a switch feels: spring length and bottom-out weight.
"What is the difference between a 67 g 23 mm long spring and a 67 g 15 mm long if not the number of coils used to achieve the same weight?"
It all comes down to the pre-tensioning. I'm not a rocket scientist so I can only use basic terms but essentially a switch spring's tension weight increases dramatically during the first 4-6 millimeters, and more or less evens out as it gets pressed towards it's bottom-out weight. By having a longer spring rated for the same bottom-out weight as a shorter spring, you essentially skip most the period of exponential weight increase, giving a more consistent weight across the switches 4mm or less of total travel. Long story short: long spring = flatter force curve and vice versa.
Conversely if we look at the other extreme side for example, a Halo True switch: it has a 12mm spring(compresses only approx. 2.7mm when assembled) rated at 95 grams bottom out, but due to its short length and despite a tactile bump it's only rated at 60 grams actuation weight because the short length allows the spring to remain at a relatively light tension during actuation. I've gone as far as to try clipping the spring length to test, but at 11mm the spring does not have enough force to reliable lift past the tactile bump and reset when used in spacebars. The Halo True's spring is a perfect example of what should be considered a true progressive spring. They feel easy and light to actuate but surprisingly difficult to bottom out when typing.
"So what do the 'stages' in multi-stage springs do"
This is a bit beyond my level of conjecture, but the multiple stages(they are seen as the 1-3 sections of tightly-wound coils in the long springs) in these long springs helps to prevent kinking, where the extended length of the springs causes it to try and 'bend and buckle' because it cannot maintain its symmetry, causing the spring to rub against the plastic. If you've ever noticed the sound of a spring kind of 'ping or crunch'(despite lubrication) as the switch is being pressed this is likely the cause.
"So what about all these different types of switches from Sprit?"
Sprit's Progressive springs are approximately 13.4mm long, and are called progressive on the basis that their 'coils-per-centimeter' varies, with a section of higher CPC on the edges and lower CPC in the middle. This is 'supposed' to create sections of different weights in the spring as it's being pressed, the lighter sections buckling and giving way to the heavier section. While these switches do indeed function that way, giving a semblance of higher tension as the switch is pressed, if I put one in a halo true it's going to be compressed approx 4.1mm. This means that those sections of lighter spring are basically compressed first and are slightly lost before you've even placed a finger on the switch. Their Complex springs are exactly the same, but different length. If I were to have my way, I'd like to see them shorten the length and heavily increase the weight, having both the short length and the light/heavy sectioning.
Their Slow series are basically in the middle at approx 16mm, with the extreme just changing the length a little.
It's a little late in the night to go into further detail, but I hope this could shed some light. BTW that graph they linked is an ARBITRARY ABOMINATION.

(Edited)

mrvco
500
Jul 11, 2021
I'm curious how longer springs than stock, ie pre-loaded, springs impact actuation feel. I've had outstanding results spring-swapping my Halo True and Clear switches with 62g gold Durock springs... for my tastes, the Halo switches went from 'unpleasant' (being kind) to easily my favorite tactile switch.
Duckferd
15
Jul 12, 2021
mrvcoThere are two 'problems' with the Halo switches. The first is the Clears have a 78g bottom out force and the Trues are even worse at 100g. The second is that (as part of the design of being a short spring), the actuation force of these switches are reasonable at around 52/54g, but the huge ramp rate brought about by the short spring design make these switches tiring to type on if you bottom them out (you are supposed to "bounce" touch type on them).
Making the switch to 62g springs decreases bottom out force required, but the actuation point force is probably still in the 52/54g range (speculating since preload force is not listed and actuation force varies depending on switch). The smaller difference between actuation and bottom out force makes it feel more linear; the lower bottom out force also makes it less fatiguing to type on.
Showing 17 of 26
Recent Activity